Altın Oran Nedir? Altın Oran Örnekleri DNA ve Evrenin Güzelliği

DNA'dan Dalgalara, Evrenin Güzellik Ölçütü: Altın Oran

Hücrelerden DNA'ya, dalgalardan salyangozlara tek bir oranın ölçüt olması mümkün mü? İşte Da Vinci'den, ünlü bilim insanlarına yüzlerce yıldır rehberlik eden altın oran.

Etrafımızda gördüğümüz her nesne, her canlı, her eser belli bir ölçüye ve orana sahip. Güzellik anlayışımızı da belki bu oranlar şekillendiriyor olabilir.

Altın Oran Nedir?

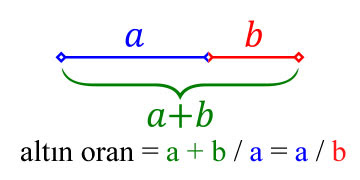
Altın oran Antik Mısır ve Yunan uygarlıklarında keşfedilmiş ve kullanılmış olan geometrik ve sayısal oran bağıntısıdır. En kısa şekilde tarif etmek gerekirse aşağıdaki görselde görebileceğiniz üzere bir doğru parçasını altın orana göre bölmek istediğinizde öyle bir noktadan bölmelisiniz ki bütünün büyük parçaya oranı, büyük parçanın küçük parçaya oranına eşit olmalıdır. Yani 1,618

Peki ya “altın oranı” hiç duydunuz mu? Duymadıysanız görmüşsünüzdür, çünkü doğanın her yerinde saklı.

Parmaklarınız, ayçiçeği, piramitler ve Mona Lisa tablosunun bir ortak yanı varsa o da altın orandır. Altın oran, Fibonacci’nin ortaya koyduğu 1,618 sayısıdır. Yani ortak noktamız matematiksel bir orantıdır diyebiliriz.

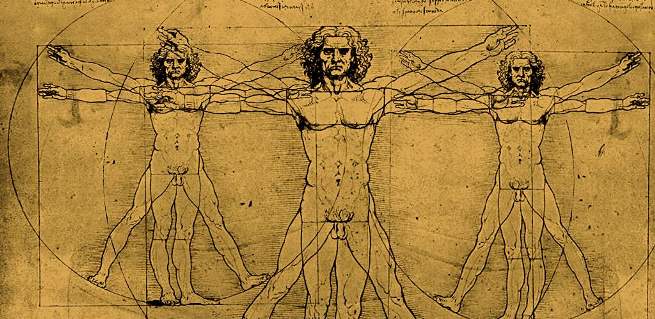
Sanatçılardan bilim insanlarına, insan vücuduyla ilgilenen profesyoneller halen 1,618'i, yani altın oranı rehber olarak alır. Leonardo Da Vinci insan anatomisini resmederken de altın oranı baz almıştır. İnsan bedeninin çeşitli kısımları ve arasındaki mesafeler de altın orana uygundur. Örneğin parmağınız üç boğuma sahiptir; parmağınızın tam boyu ile ilk iki boğumu arasında bile altın oran söz konusudur. 

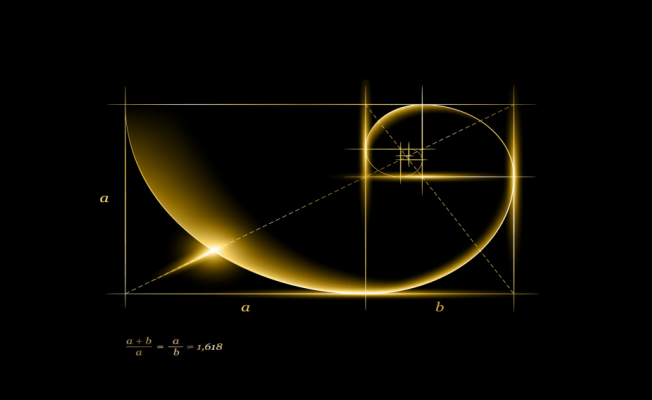
Peki sarmal görünüme sahip objeler, köşeli objelere göre daha ilgi çekici görünmüyor mu? Bunun nedeni doğadaki sarmal yapıda olan deniz kabuğu, ayçiçeği, kozalak gibi birçok yapının altın dikdörtgendeki sarmal tasarımın oranında oluşmuş olması. Koç boynuzundaki sarmallardan, salyangozun kabuğuna doğanın her yerinde altın oran karşımıza çıkıyor.

Yönümüzü biraz daha küçük ebatlara çevirelim. Her bir kar kristali yakından incelendiğinde altın oranı verir. Biraz daha küçüklere gidelim. DNA! İki sarmaldan oluşan DNA’ların uzunluğu 34 angström, genişliği ise 21 angström’dür. Bunlar art arda gelen iki Fibonacci sayısıdır. Evrenin birçok noktasında yer alan altın oran, sanat ve matematiği birleştiren doğanın güzelliğinin bir ölçüsüdür de diyebiliriz.

Altın Oran Örnekleri

İnsan Kafası: Bildiğiniz gibi her insanın kafasında bir ya da birden fazla saçların çıktığı düğüm noktası denilen bir nokta vardır. İşte bu noktadan çıkan saçlar doğrusal yani dik değil, bir spiral, bir eğri yaparak çıkmaktadır. İşte bu spiralin ya da eğrinin tanjantı yani eğrilik açısı bize altın oranı verecektir.

Papatya Çiçeği: Papatya Çiçeğinde de ayçiçeğinde olduğu gibi bir altın oran mevcuttur.

Ayçiçeği: Ayçiçeği’nin merkezinden dışarıya doğru sağdan sola ve soldan sağa doğru tane sayılarının birbrine oranı altın oranı verir

İnsan Vücudu: İnsan vücudunun bir parçası olan kolları dirsek iki bölüme ayırır(Büyük(üst) bölüm ve küçük(alt) bölüm olarak). Kolumuzun üst bölü- münün alt bölüme oranı altın oranı verceği gibi, kolumuzun tamamının üst bölüme oranı yine altın oranı verir.

Parmaklar: Ellerimizdeki parmaklarla altın oranın ne alakası var diyebilirsiniz. İşte size alaka… Parmaklarınızın üst boğumunun alt boğuma oranı altın oranı vereceği gibi, parmağınızın tamamının üst boğuma oranı yine altın oranı verir.

Mısır Piramitleri: İşte size Altın Oran’ın en eski örneklerinden biri… Şimdi ne alaka Altın Oran ve Milattan Önce yapılan Mısır Piramitleri? Alaka şu; Her bir piramitin tabanının yüksekliğine oranı evet yine altın oranı veriyor.

Picasso: Picasso da Leonardo da Vinci gibi ünlü bir ressamdır. Ve resimlerinde bu oranı kullanmıştır.

Çam Kozalağı: Çam kozalağındaki taneler kozalağın altındaki sabit bir noktadan kozalağın tepesindeki başka bir sabit noktaya doğru spiraller (eğriler) oluşturarak çıkarlar. İşte bu eğrinin eğrilik açısı altın orandır.

Deniz Kabuğu: Denize çoğumuz gitmişizdir. Deniz kabuklarına dikkat edenimiz, belki de kolleksiyon yapanımız vardır. İşte deniz kabuğunun yapısı incelendiğinde bir eğrilik tespit edilmiş ve bu eğriliğin tanjantının altın oran olduğu görülmüştür.

Mimar Sinan: Mimar Sinan’ın da bir çok eserinde bu altın oran görülmektedir. Mesela Süleymaniye ve Selimiye Camileri’nin minarelerinde bu oran görülmektedir

Leonardo da Vinci: Bilindiği gibi Leonardo da Vinci Rönesans devri ünlü ressamlarındandır. Şimdi bu ünlü ressamın çizmiş oolduğu tabloları inceleyelim. Mona Lisa: Bu tablonun boyunun enine oranı altın oranı verir. Aziz Jerome: Yine tablonun boyunun enine oranı bize altın oranı verir.

Tütün Bitkisi: Tütün Bitkisinin yapraklarının dizilişinde bir eğrilik söz konusudur. Bu eğriliğin tanjantı altın orandır.

Eğrelti Otu: Tütün Bitkisindeki aynı özellik Eğrelti Otu’nda da vardır.

Elektrik Devresi: Ya demek ki Altın Oran sadece Matematik ve kainatta değil, Fizik’te de kullanılıyormuş. Nasıl mı? Şöyle… Verilen n tane dirençten maximum verim elde etmek için bir paralel bağlama yapılması gerekir. Bu durumda Eşdeğer Direnç, yani Reş= yani altın oran olur.

Salyangoz: Salyangozun Kabuğu bir düzleme aktarılırsa, bu düzlem bir dikdörtgen oluşturur (-ki biz bu dikdörtgene altın dikdörtgen diyoruz.-) İşte bu dikdörtgenin boyunun enine oranı yine altın oranı verir.

Otomotiv Sanayisinde: Yeni modern arabalarda ki  eğim hatlar ve estetik görünümün eğrilik açısı vardır bu altın oran hesabıyla yapılmaktadır.